I. Introduction et remerciements▲
À l'heure actuelle, si les espaces de stockage ne posent pas de réels problèmes, ce n'est pas le cas des flux de données sur les réseaux. En effet, les réseaux (Lan, Internet …) sont de plus en plus utilisés pour échanger des informations. Cela pose cependant un problème important : celui du temps de transmission. Le débit des réseaux étant limité, on cherche à réduire la taille des données à envoyer afin de rendre la transmission plus rapide et par conséquent plus satisfaisante. Pour cela, il existe deux méthodes.
La première, qui engendre une perte ou une altération de l'information, est utilisée pour tout ce qui concerne l'image et le son. Elle consiste dans un premier temps à enlever toute l'information à laquelle les capteurs humains ne sont pas sensibles (fréquences inaudibles, surfaces insignifiantes …) puis à écrire une nouvelle donnée qui ne pourra plus reprendre son format (qualité) original. Il y a eu suppression de l'information de manière irréversible.
La seconde est dite « lossless », c'est-à-dire sans perte et elle est appliquée dans tous les domaines ou la perte d'information est inacceptable : exécutables, textes … Elle consiste à analyser des données et à en déduire une écriture de taille inférieure. L'une de ces méthodes est appelée compression de Huffman (inventée par le mathématicien du même nom) et c'est celle que nous allons étudier ci-après.
Je tiens à préciser que cet article a été écrit grâce à la généreuse participation de GoldenEye qui nous éclaire régulièrement de ses lumières sur notre forum.
Je tiens à remercier fearyourselffearyourself pour sa relecture et milliemillie pour la mise en page.
II. Présentation▲
La méthode de compression Huffman consiste à diminuer au maximum le nombre de bits utilisés pour coder un fragment d'information. Prenons l'exemple d'un fichier de texte : le fragment d'information sera un caractère ou une suite de caractères. Plus le fragment sera grand, plus les possibilités seront grandes et donc la mise en œuvre complexe à exécuter. L'algorithme de Huffman se base sur la fréquence d'apparition d'un fragment pour le coder : plus un fragment est fréquent, moins on utilisera de bits pour le coder. Dans notre exemple de fichier texte, si on considère que notre fragment est la taille d'un caractère, on peut remarquer que certaines voyelles sont beaucoup plus fréquentes que certaines consonnes : par exemple la lettre ‘e' est largement plus fréquente que la lettre ‘x' par conséquent la lettre ‘e' sera peut-être codée sur 2 bits alors que la lettre ‘x' en prendra 10.
Pour pouvoir compresser puis décompresser l'information, on va donc devoir utiliser une table de fréquences et deux choix s'offrent à nous : calculer une table et l'intégrer au fichier ou utiliser une table générique intégrée dans la fonction de compression. Dans le premier cas, la compression est meilleure puisqu'elle est adaptée au fichier à compresser, mais elle nécessite le calcul d'une table de fréquences et le fichier sera plus important également du fait de la présence de cette table dans le fichier. Dans le second cas, la compression sera plus rapide puisqu’elle n'aura pas à calculer les fréquences, par contre l'efficacité de la compression sera moindre et le gain obtenu par la première méthode (ratio de compression + taille de la table) peut être supérieur à celui de la deuxième (ratio de compression).
III. Création de la table des fréquences d'apparition des fragments▲
Cette table consiste en un comptage empirique des fragments au sein des données à compresser. Reprenons l'exemple d'un texte : nous allons analyser la phrase :
« gRRosminet et GoldenEye programment Huffman »
Pour simplifier l'exemple, nous ignorerons la casse :
|
Lettres |
Occurrences |
Fréquence |
|---|---|---|
|
G |
3 |
4,14% |
|
O |
3 |
7,14% |
|
S |
1 |
2,38% |
|
M |
4 |
9,52% |
|
I |
1 |
2,38% |
|
N |
4 |
9,52% |
|
E |
6 |
14,29% |
|
T |
3 |
7,14% |
|
L |
1 |
2,38% |
|
D |
1 |
2,38% |
|
Y |
1 |
2,38% |
|
P |
1 |
2,38% |
|
A |
2 |
4,76% |
|
H |
1 |
2,38% |
|
U |
1 |
2,38% |
|
F |
2 |
4,76% |
|
[ESPACE] |
4 |
9,52% |
|
Total |
42 |
100% |
IV. Création de l'arbre de Huffman▲
L'arbre de Huffman est la structure données qui va nous permettre de donner un code pour chaque lettre en fonction de sa fréquence.
IV-A. Étape 1▲
Il faut commencer par trier la liste par ordre croissant de fréquences (vous remarquerez que le tri a été fait sur la fréquence puis sur la lettre ce qui sera important pour permettre la diminution de la taille de l'entête) :
|
Lettres |
Occurrences |
Fréquence |
|---|---|---|
|
D |
1 |
2,38% |
|
H |
1 |
2,38% |
|
I |
1 |
2,38% |
|
L |
1 |
2,38% |
|
P |
1 |
2,38% |
|
S |
1 |
2,38% |
|
U |
1 |
2,38% |
|
Y |
1 |
2,38% |
|
A |
2 |
4,76% |
|
F |
2 |
4,76% |
|
G |
3 |
7,14% |
|
O |
3 |
7,14% |
|
R |
3 |
7,14% |
|
T |
3 |
7,14% |
|
[ESPACE] |
4 |
9,52% |
|
M |
4 |
9,52% |
|
N |
4 |
9,52% |
|
E |
6 |
14,29% |
Nous allons maintenant construire un nœud de l'arbre pour chaque fragment et les placer dans une liste ordonnée de nœuds. Un nœud doit avoir une structure telle que ci-contre :
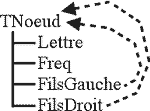
IV-B. Étape 2▲
Nous allons maintenant construire l'arbre à partir de la liste ordonnée de nœuds. La construction est très facile : il suffit de prendre les deux nœuds les moins fréquents (D et H) et de les ajouter comme fils d'un nouveau nœud qui aura pour fréquence la somme des deux.
Il suffit de réitérer cette étape jusqu'à ne plus avoir qu'un seul nœud. Après cela, descendre vers la gauche équivaut à un 0, et descendre vers la droite à un 1.
On en déduit le codage suivant :
|
Lettres |
Occurrences |
Fréquence |
Codage |
|---|---|---|---|
|
D |
1 |
6 |
111000 |
|
H |
1 |
6 |
111001 |
|
I |
1 |
6 |
111010 |
|
L |
1 |
6 |
111011 |
|
P |
1 |
6 |
111100 |
|
S |
1 |
6 |
111101 |
|
U |
1 |
6 |
111110 |
|
Y |
1 |
6 |
111111 |
|
A |
2 |
4 |
0000 |
|
F |
2 |
4 |
0001 |
|
G |
3 |
4 |
1000 |
|
O |
3 |
4 |
1001 |
|
R |
3 |
4 |
1010 |
|
T |
3 |
4 |
1011 |
|
[ESPACE] |
4 |
3 |
001 |
|
M |
4 |
3 |
010 |
|
N |
4 |
3 |
011 |
|
E |
6 |
3 |
110 |
|
Total de bits (normal | compressé) |
336 |
166 |
La dernière ligne du tableau nous montre qu'une fois compressée, la phrase n'occupe même plus la moitié de l'espace original (hors entête).
V. Compression / Décompression▲
V-A. Compression▲
Pour la compression des données, on va donc devoir écrire un nouveau fichier contenant deux parties : l'entête et les données compressées. L'entête : il doit contenir le nom original du fichier, la taille originale et une table de correspondance qui permette de reconstituer le fichier original (cf table précédente).
Pour compresser les données, on va donc lire le fichier original fragment par fragment (ici octet par octet) et on écrira le code Huffman correspondant dans le fichier de destination. Attention, les codes de Huffman ne font pas toujours un multiple de 8 bits et par conséquent ils nécessitent d'être mis dans une zone tampon avant d'être écris dans le fichier ! Vous pouvez par exemple utiliser un tableau de 8 caractères qui contienne soit '1' soit '0', mais cela n'est qu'une proposition et l'objectif n'est pas de vous aider à programmer, mais de vous faire comprendre le fonctionnement donc pour les plus perdus voyez les applications proposées.
V-B. Décompression▲
Pour la décompression, vous lirez l'entête du fichier, puis, pour chaque bit lu, vous descendrez dans votre arbre et à chaque feuille terminale, vous aurez décodé un caractère original que vous pourrez écrire dans le fichier de restitution.
VI. Remarques▲
On définit le ratio de compression :
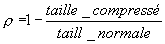
Ici
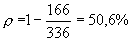
En règle générale, un fichier texte sans pathologie particulière est compressé par cette méthode suivant un ratio de 30 à 60 %.
Sur de très petits fichiers ( moins de 1 Ko), l'entête est assez volumineux par rapport aux informations compressées. Le fichier réduit a alors une taille supérieure au fichier original…
Sur de gros fichiers, on peut appliquer l'algorithme de Huffman non pas caractère par caractère, mais par tranche de 2, 3 ou 4 caractères. Le problème est que la construction de l'arbre prend beaucoup plus de temps (l'arbre est plus gros,il y a 65 536 doublets possibles de caractères ASCII étendu par exemple). De même, l'entête prend une place considérable.